11 有理数 無理数の問題 京極一樹の数学塾
このページは、 小学6年生で習う「整数×分数の約分のある掛け算の問題集」が無料でダウンロードできる ページです。 この問題のポイント ・ 整数に、分数を掛ける計算をします。 ・整数と分数の掛け算では、下の例のように整数を分子に掛けることで、計算ができます。 = = = 2 × 3 5 = 2 × 3 5 = 6 5 ( = 1 1 5) ・約分ができるときは、計算の途中で約分するのがポイントです。 ぴよ校長 整数に (問題②) 8÷ 整数8を に、帯分数 を仮分数 に直すところからはじめます。 計算のとちゅうで分子・分母ともに2で約分できるので、約分をしながら計算します。 =8÷ = × = = = 答え または (問題③) ÷ ÷6 帯分数 を仮分数 に、整数6を に直すところ
整数 分数 問題
整数 分数 問題- つまり整数×分数の計算は「分子と整数をかけ算すれば良い」ということになります。 整数×分数の計算のやり方だけでなく、なぜのそのような解き方になるのかを理解できるように教えてあげてください。 整数÷分数の意味を理解しましょう 次に先ほどの × = = = 答え (問題②) 整数を分数にするときには分母が1の仮分数と考えます。(例:1= 、2= ) この問題では3= と考えて計算をします。 × = = 答え または (問題③) × × 帯分数は仮分数に直し、約分できるときには約分をしながら計算をします。 ×

分数形の不定方程式の解き方をイチから解説 数スタ
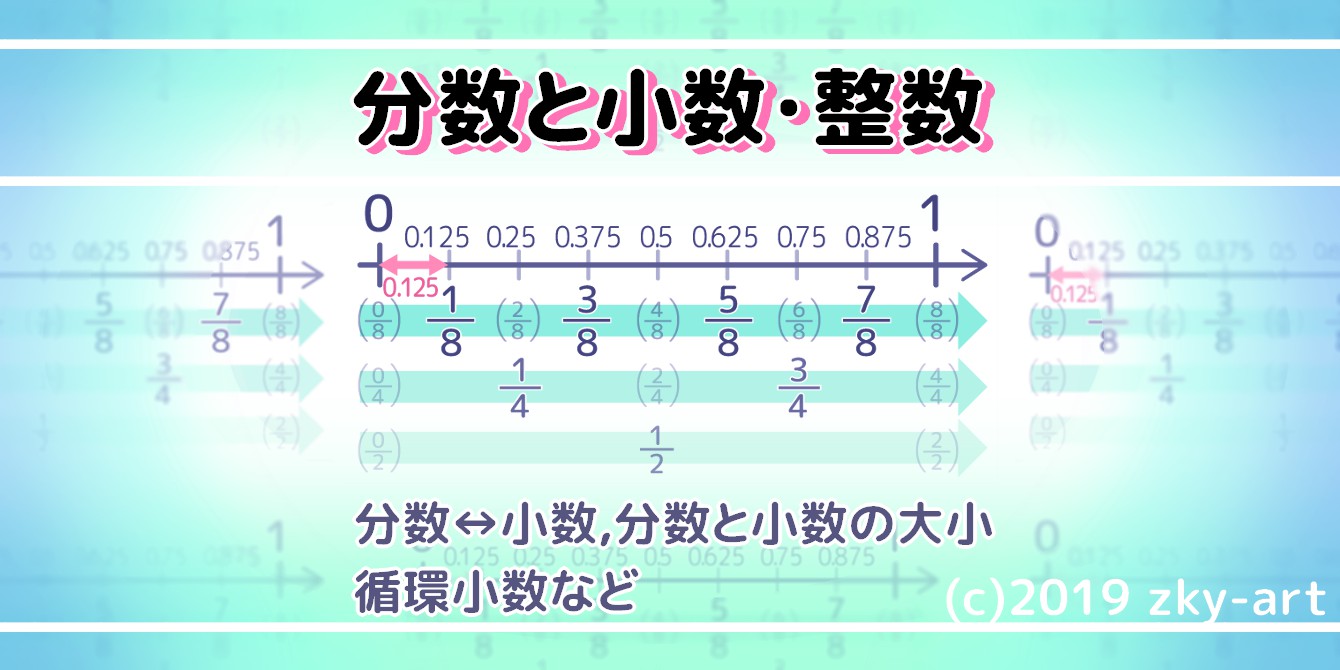
→ 5年生の分数×整数 の問題はこちら 練習問題をダウンロード 画像をクリックするとPDFファイルをダウンロード出来ます。 分数のかけ算基本 1は約分なし。 2は片方、3は両方約分します。 先に約分してから分母どうし、分子どうしのかけ算をしましょう。 分数×分数練習1 分数×分数練習2 分数×分数 3つの数のかけ算 → 分数÷分数 いっきに極める算数 4 小学4~6年の分数の計算 新品無学年で分数に関する演習をする計算プリントです。 進級テストつき!分数計算トレーニング (無学年) ・仮分数⇔帯分数 ・等しい分数 ・倍数/公倍数 ・約数/公約数 ・約分/通分 ・同分母たし算/引き算 ・分数のたし算/引き算 ・分数のかけ算 ・分数のわり算・10回のテスト形式で計算力を 求六年级分数乘法口算题不要答案的最好是分数乘以整数的 以下文字资料是由(历史新知网wwwlishixinzhicom)小编为大家搜集整理后发布的内容,让我们赶快一起来看一下吧! 1 3/7 × 49/9 4/3 2 8/9 × 15/36 1/27 3 12× 5/6 – 2/9 ×3 4 8× 5/4 1/4 5 6÷ 3/8 – 3/8 ÷6
小学校 算数6年 分数と整数の計算 No 質問 1 真分数×整数の計算は,どのように考えるの (図で考える方法) 2 真分数×整数の計算は,なぜ,整数を分子にかけるの(図で考える方法) 3 真分数×整数の計算は,どのようにするの(計算方法) 問題の式は、整数と分数のかけ算じゃな ☆ポイントは、整数×分数は、整数を分子にかけ算すればいい \( 9×( \frac{4}{3} ) \) \( = – \frac{9×4}{3} \) とやるわけじゃな 整数と分数の約分ありの掛け算の解き方 それでは早速例題をみていきましょう。 例題 次の計算をしてしましょう。 $$ (1)4\times \frac {3} {7} (2)8\times \frac {5} {12}$$ $$ (1)4\times \frac {3} {7}$$からみていきましょう。 約分なしの計算問題を入れてみました。 まずはこれができなければ進めません。 そのまま計算する 「整数×分数」の計算は整数と分子を掛けることで計算すること
整数 分数 問題のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |
 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す | 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |
 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す | 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |
「整数 分数 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |
 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |
 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |
「整数 分数 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
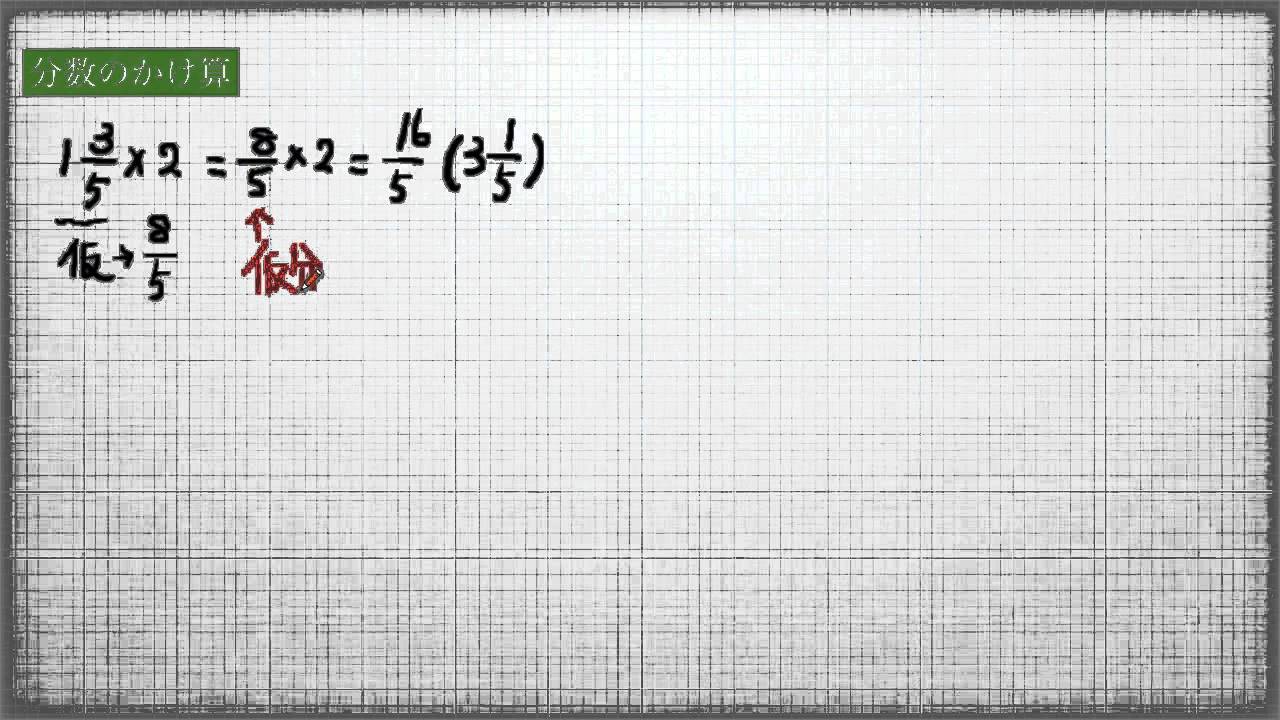 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |
 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |
 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |
「整数 分数 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |
 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す | 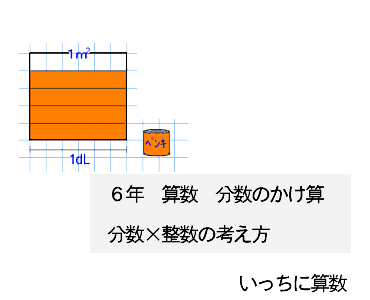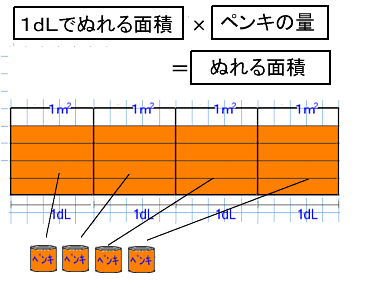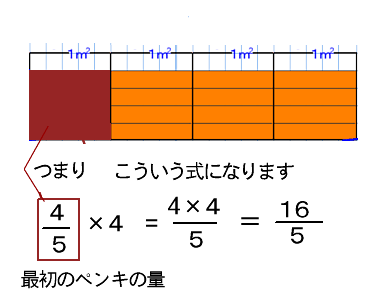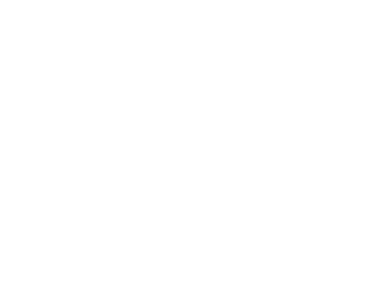 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す | 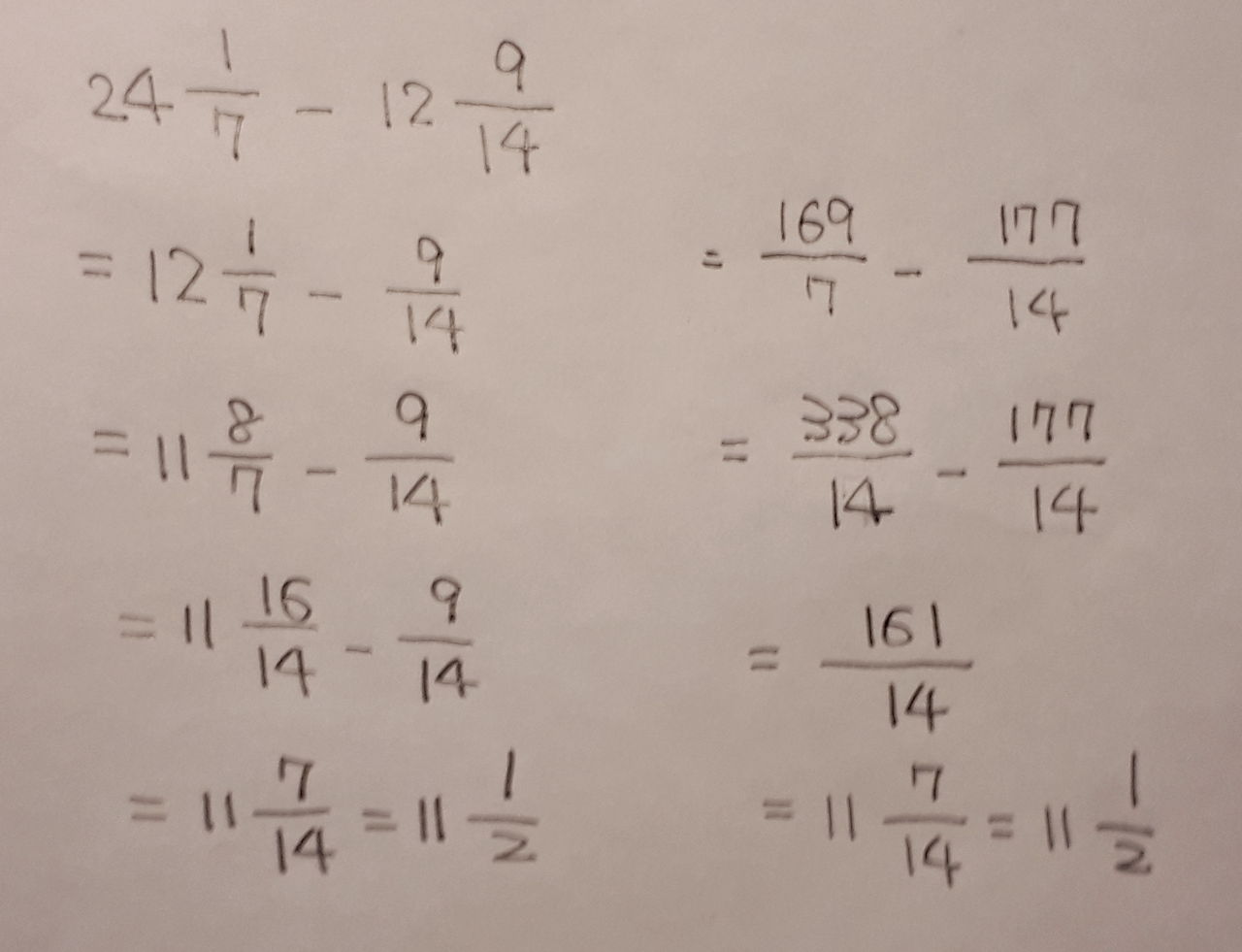 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |
 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す | 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |
「整数 分数 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す | 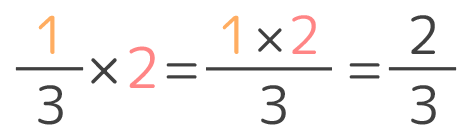 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |
 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す | 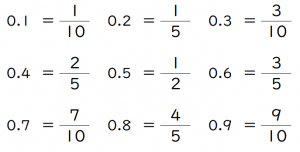 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |
 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す | 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す | 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |
「整数 分数 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す | 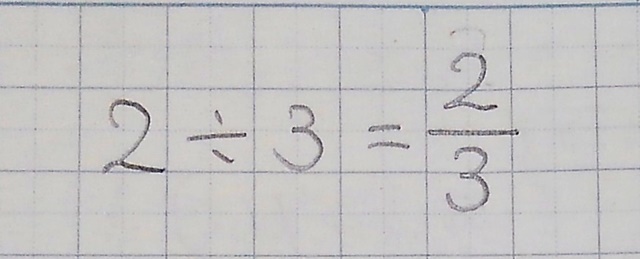 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |
 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |
 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |
「整数 分数 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |
 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |
分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す | 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |
「整数 分数 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
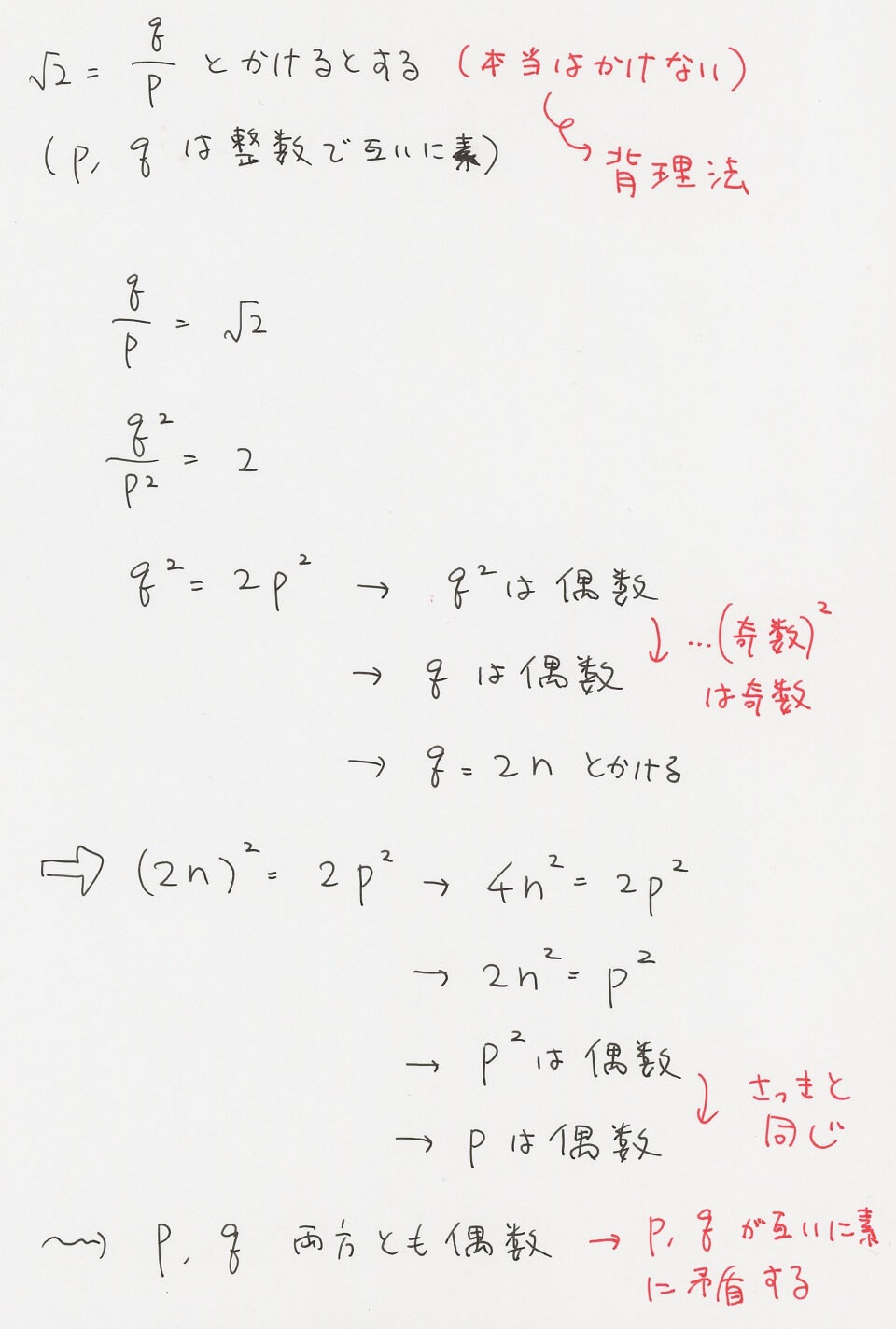 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す | 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |
 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す | 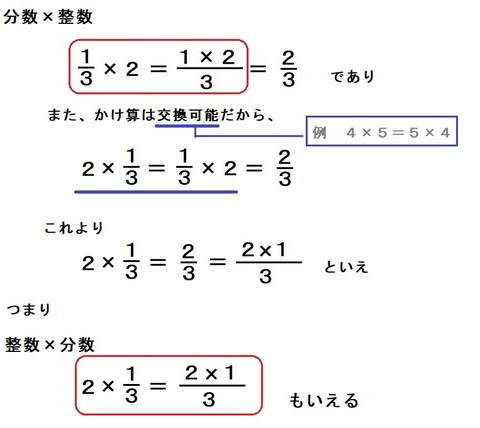 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す | 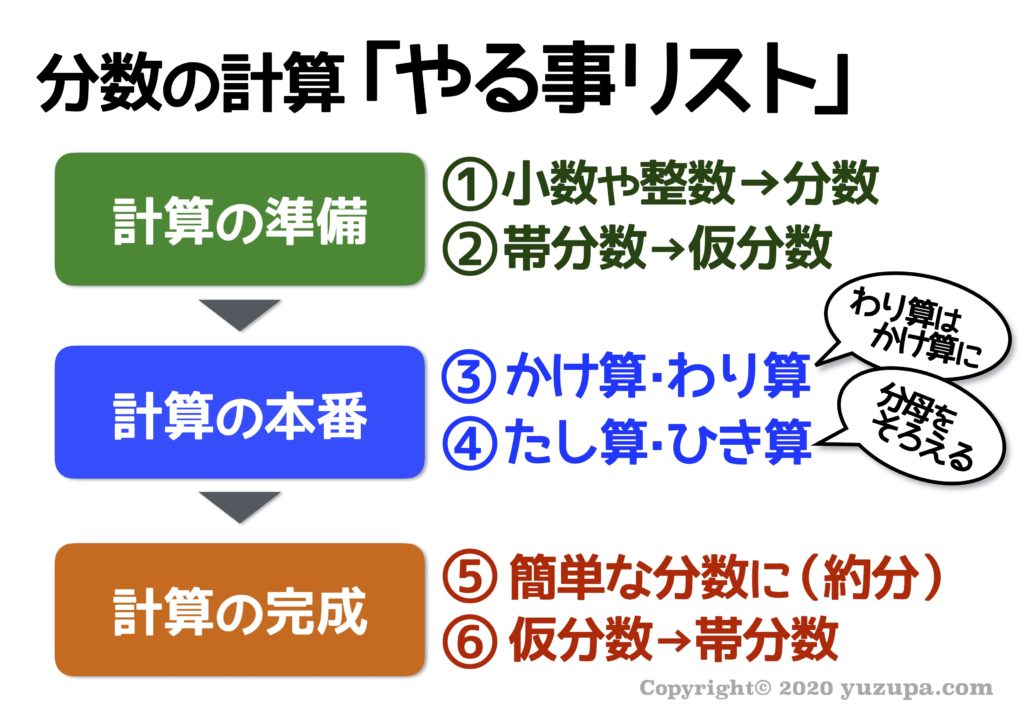 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |
 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |
「整数 分数 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |
 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |
分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す | 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |
「整数 分数 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |
 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |
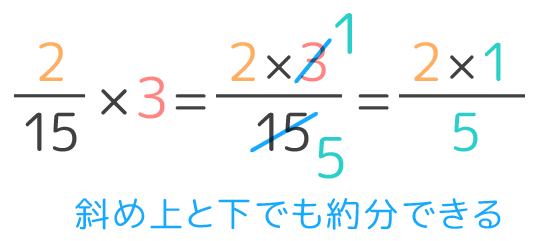 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す | 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す | 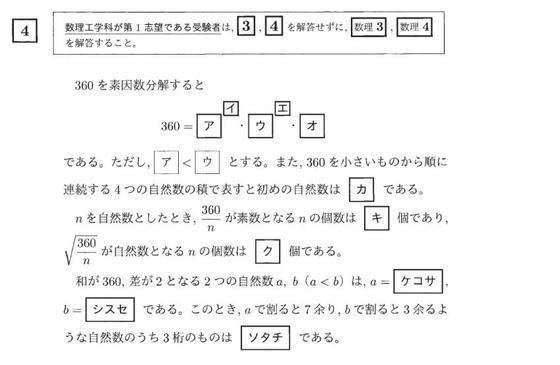 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |
「整数 分数 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す | 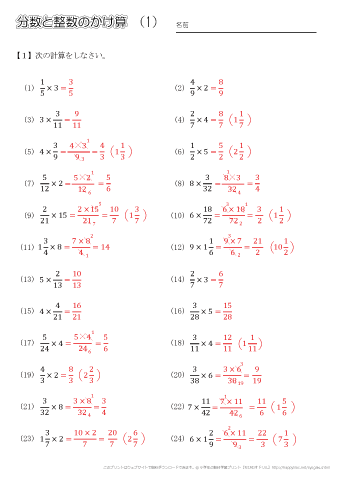 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す | 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |
 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |
 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す | 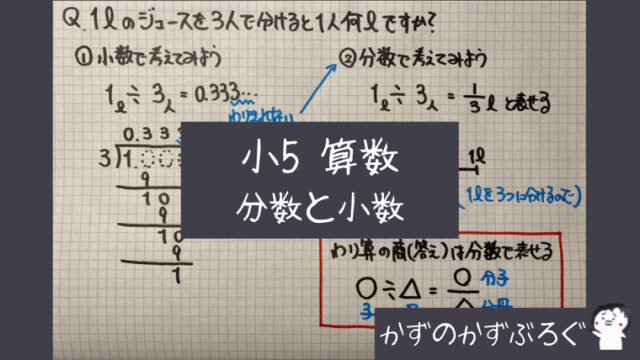 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |
「整数 分数 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |
 分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |  分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す |
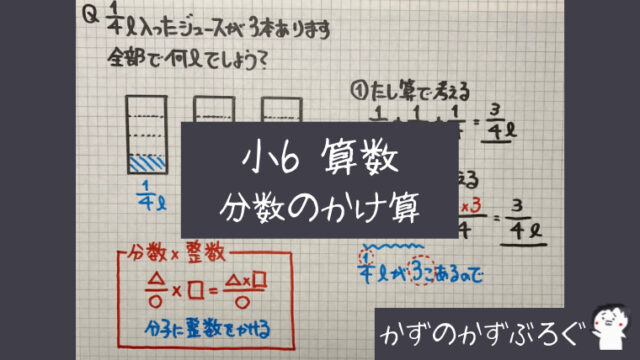
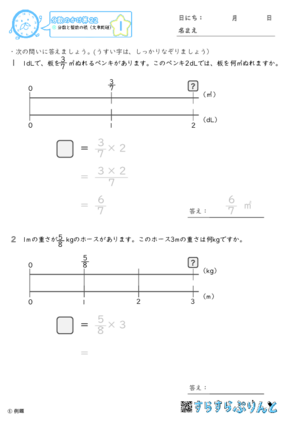
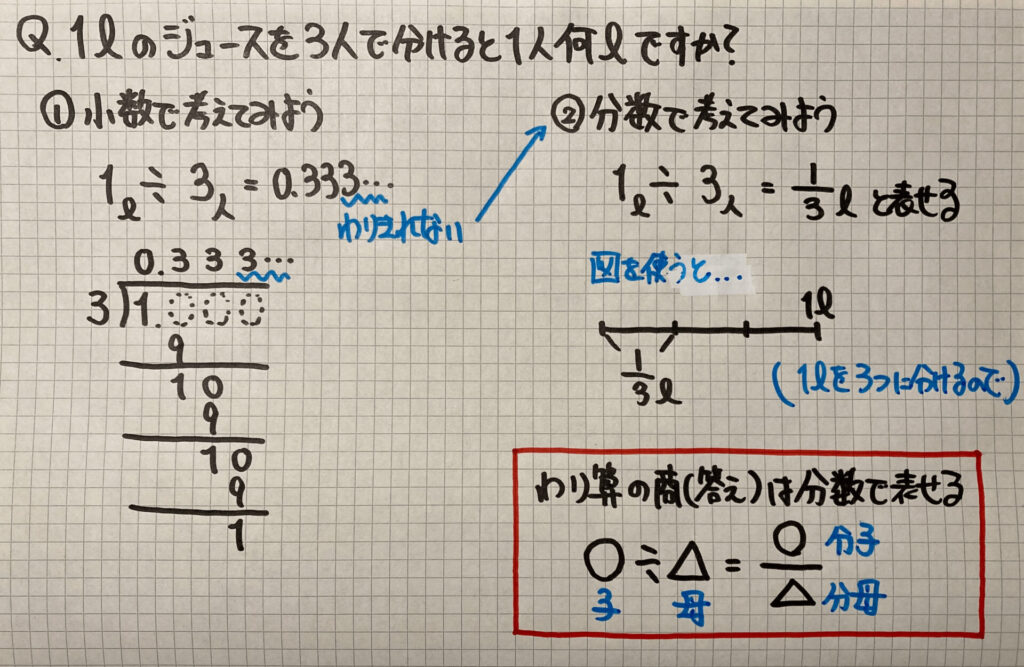
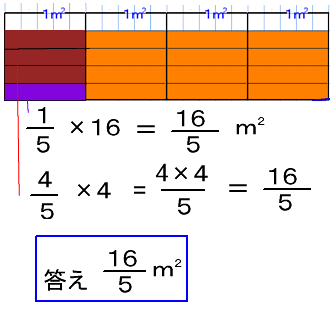
第 回 1 1分数×整数の計算 分数のかけ算とわり算 1 dl で,板を 3 5 m2ぬれるペンキがあります。 このペンキ2 dl でぬれる板の面積を考え ます。 ペンキでぬれる面積は, ペンキ1 dl でぬれる面積(m2) ×ペンキの量(dl) で求められるので,式は, 3 5 ×2 となります。 この式の計算の仕方を考えてみましょう。 2 3 5 ×2 m は,図2のように表されます。 3 5 2m は 1 5 m2の3個 こ 分だから, 3 5 ×2分数の掛け算 小学5年生 分数×整数 小学6年生 分数×分数 小学6年生 帯分数×帯分数 分数の割り算 小学5年生 分数÷整数 小学6年生 分数÷分数 小学6年生 帯分数÷帯分数 小学5年生 分数の約分 小学5年生 分数の通分 小学4年生 帯分数⇔仮分数の変換 小学5年生 分数⇔小数の変換 約数・倍数 小学5年生 最大公約数を見つける練習問題 小学5年生 最小公倍数を見つける練習問題 平面図形 四角形・三角形 小
Incoming Term: 整数 分数 問題, 整数 小数 分数 問題, 分数 整数 問題 答え 付き, 分数 割り算 整数 問題,




0 件のコメント:
コメントを投稿